Connections Between GANs and AC Methods in RL

---

* 본 게시글은 원작자에게 허락을 받아 번역한 글입니다. 원 게시글은 이곳에 있습니다. 심한 번역체를 이해하며 읽어주세요.... 참고한 논문은 'Connecting Generative Adversarial Networks and Actor-Critic Methods(David Pfau, Oriol Vinyals)' 이며 다운은 이곳에서 받을 수 있습니다.

---

 

 

  처음 ‘Generative Adversarial Nets’(이하 GAN) 논문을 읽었을 때, 강화학습과 GAN 사이에 뭔가 모를 연결점이 있다고 느꼈다. 몇번의 연구 이후에, 우연히 DeepMind의 David Pfau와 Oriol Vinyals가 2017년 진행한 연구를 발견하게 됐다.

  논문에서 볼 수 있듯, 먼저 두 methods가 무엇인지에 대한 리뷰를 한 뒤 그 사이의 connection을 설명할 예정이다. 보본 글의 목표는 그 connection을 이해하기 쉽게 설명하는 것이다.

 

1 Generative Adversarial Nets

  GAN은 2014년 Goodfellow에 의해 소개된 생성 모델이다. 이는 input-output relationships을 가지는 generator(이하 생성자) G와 discriminator(이하 판별자) D 사이의 minmax game에 따른다.

• G는 latent z를 input으로 가져와 synthetic data Xgen 를 output으로 내놓는다. Input z는 보통 zero-mean identity-covariance multivariate Gaussian N(0,1) 으로부터 샘플링되고 output Xgen 은 보통 이미지이다.
• D는 real data Xreal 과 synthetic data Xgen 를 input으로 취하며 실제 입력 확률을 output으로 가진다. 따라서 output은 기본적으로 0과 1사이의 단일 스칼라 값이다.

  각 training cycle에서, 판별자 D가 판별하는 동안 생성자 G는 D를 더 잘 속이기 위해 노력한다. GANs의 전형적인 high-level architecture는 Fig.1과 같다.

 

 

공식적으로, value function V(D,G)를 따르는 minmax 게임은 G와 D사이에서 play된다:

So, in each training iteration:

• D는 loss LDD,G 를 최대화하기 위해 try한다: 

• G는 loss LGD,G 를 최대화하기 위해 try한다:

Note: The first term is thrown away in L_G(D,G)  since it is just a constant for G.

 

  GAN 논문에서, log(1-D(G(z) ))의 기대 값을 최소화하는 대신 logD(X) 의 기대 값을 최대화하는 트릭을 제안한다. 트릭의 아이디어는 학습 초기 단계에서 포화된 gradient가 발생하는 것을 방지하는 것이다.

(만약 이것이 명확하지 않다면, 단순히 D(G(z)) -> 0을 상상해보고 L_G(D,G )가 논의된 losses 중 2개일 때 ∇θGLGD,G 를 확인할 수 있다. 이때 제안된 tricky loss는 D가 더 똑똑 해질 때 G를 더 많이 처벌할 가능성이 있다는 것을 볼 수 있다.)

•  여기서 saturated gradients가 의미하는 바는 아직 잘 모르겠다.
•  중간에 losses 중 2개가 의미하는 부분은 G와 D의 loss가 같은 값을 가진다는 의미인지는 약간 헷갈린다.

  또한 최대화 문제가 loss function 앞에 -를 붙이면서 최소화 문제가 될 수 있다는 것을 알아야 한다.

  따라서, 위와 같은 트릭을 이용하면 문제를 bilevel minimization problem 즉 각각의 training iteration에서 바뀔 수 있다.

• D는 loss LDD,G 를 최소화하기 위해 try한다:

• G는 loss LGD,G 를 최소화하기 위해 try한다:

  At optimal convergence, G는 실제처럼 보이는 data를 만들어 내길 기대하고 D는 만들어진 data와 실제 data 사이의 차이를 알 수 없으므로 0.5를 출력한다.

 

 

2 Actor-Critic Methods

  Actor-Critic methods(이하 AC)는 가치 기반 학습법(as 가치 이터레이션, MC moethods and TD-learning)과 정책 기반 학습법(as policy gradients)의 결합인 강화학습의 method이다. 여러 AC의 methods가 있지만, 본 글에선 critic이 행동 가치 함수인 Q(s,a)를 출력하고 actor가 policy π 를 출력하는 것에 초점을 맞출 것이다.

(그 이유는 Section3에서 알 수 있다.) Pfau와 Vinyals의 연구에서 고려된 방법은 Deterministic Policy Gradients(DPG), Stochastic Value Gradients(SVG) 그리고 Neurally-Fitted Q-Learning with Continuous Actions(NFQCA)이다. GAN과 연관이 있는 것을 선택하는 것은 중요하지 않으므로, DPG와의 discussion을 계속하고 그것을 AC 방법과 바꾸어 사용할 것이다.

Note: 유명한 AC 방법 중 하나인 Asynchronous Advantage Actor-Critic(A3C)는 discrete action space와 continuous action space 모두에서 좋은 결과를 보여줬지만, A3C의 critic은 state value function V(s)를 출력한다. V(s)는 action에 대한 어떠한 정보도 포함하고 있지 않기 때문에 actor에 gradients를 전달할 수 없다. 이러한 이유로 A3C는 Section 3에서 설명할 setting과는 맞지 않는다.

 

  DPG 타입의 AC methods에는 actor A 와 critic C라고 불리우는 두 개의 neural nets이 있다. 이번에는 minimax game이 없고, 아래와 같은 input-output 관계를 가진다.

• A는 state s_t 를 입력으로 가지고 policy π 를 출력한다. 이 policy는 deterministic(DPG, 결정적)일 수도 stochastic(SVG, 확률적)일 수도 있다.
• C는 state s_t 를 입력으로 가지고 A에서 policy π 에 따라 action a가 선택되는 action-value function Q(s_t, a_t )를 출력한다.

  각각의 학습 사이클에서, actor A는 최적의 policy를 예측할 때 더 나아지며 critic C는 state-action value function Q(s,a)를 근사할 때 더 나아진다. DPG 타입 AC methods의 일반적인 high-level architecture는 Fig.2와 같다.

Fig.2. DPG  타입  methods 의  Architecture.  실선은  data flow 를 나타내고 ,  점선은  gradient flow 를 나타냄 . Critic 은  actor 로부터  data 를 생성된 데이터를 사용한다 .  그후  gradients 가 계산되고  networks 의 변수로 전달된다 .  이것은  actor 가 좋은  policies 를 배우고  critic 이 미래  rewards 에 대한 좋은 예측을 할 때까지 계속 반복된다 .

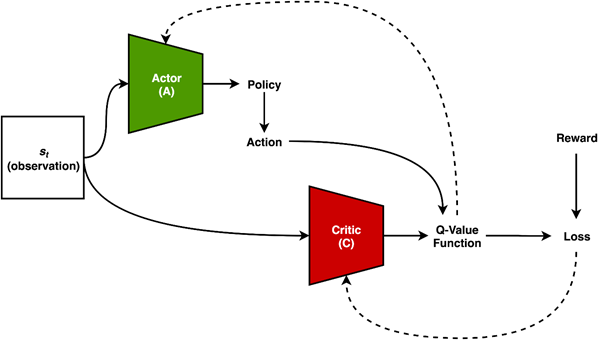
MDP는 아래와 같다.

• State S
• Action A
• Distribution over initial state p0(s)
• Transition function P(st+1|st,at)
• Reward distribution Rst
• Discount factor γ

  그리고 action-value function Q(s,a)는 주어진 policy에 대해 아래와 같이 정의된다.

그리고 최적의 policy인 π* 는 Qπ (s,a)로부터 아래와 같이 얻어질 수 있다.

  DPG 타입 methods의 학습 순서는 또한 모든 훈련 단계에서 bilevel minimization problem으로 표현될 수 있다.

• C는 loss L_C(Q,π) 를 최소화한다.

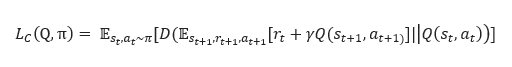
• A는 loss  L_A(Q,π) 를 최소화한다.

Note: Q( . ) ≡  C( . ) and π . ≡A..D(.|.  is any non-negative divergence.

()

최적의 수렴에서, A는 총 discounted future reward를 최대화하는 polices를 생성할 것으로 기대되며, C는 미래의 좋은 예언자가 될 것을 기대 받는다.

 

 

3 Connection

  먼저, GANs과 AC methods 둘 다 오직 하나의 신경만만이 환경으로부터 reward signals을 인식한다는 것을 주목하자. (D in GANs and C in AC) 또 다른 신경만은 (G in GANs and A in AC) 오직 첫번째 네트워크의 gradients를 통해 정보를 획득한다. 이러한 두 방법의 high level 정보 흐름 구조는 Fig.3와 같다.

Fig.3. (a)는 GAN (b)는 AC의 정보 흐름. 위와 동일하게 실선은 data flow, 점선은 gradient flow를 나타냄. Analogous flow는 빨간색으로 표시됨. 두 methods 모두 하나의 네트워크는 환경으로부터 오는 reward 정보를 받아들이고 나머지 네트워크는 받아들여진 정보로부터 온 gradient를 이용한다.

  GAN game(minimax game)에서 RL setting으로 옮기고, D를 C로 G를 A로 처리하면 그 connection을 더 자세히 설명할 수 있다. 이 연구에서, Pfau와 Vinyals가 정의한 MDP는 아래와 같다.

• Action은 빈 이미지에서 모든 픽셀의 수정이다. (A는 action을 취하는 네트워크)
• State는 A로부터 생성된 이미지 또는 실제 이미지이다.
• Reward는 1(환경으로부터 실제 이미지가 선택되었을 때) 또는 0(otherwise)

Note: A로부터 얻은 action은 future states에 영향을 주지 않기 때문에, MDP는 stateless이다. (하나의 state로 action을 취하고, reward를 얻으면 게임이 끝난다.)

이제, GAN game과 비슷한 RL setting에서 AC 스타일의 학습을 할 수 있다. 하지만, 여전히 몇 수정이 필요하다.

• A는 state에 접근할 수 없다. 즉 A는 blind다. 만약 접근한다면, 모든 스텝에서 실제 이미지를 복사하고 -Es0~p0,a0~π[Qπ(s0,a0)] 를 최소화하는 법을 배운다. (오리지널 GAN에서도 G는 실제 이미지를 볼 수 없다.) A는 random latent space로부터 actions을 생성한다.
• 만약 환경으로부터 실제 이미지가 선택된다면, A는 0의 gradient를 받게 된다. (오리지널 GAN에서 G의 loss는 실제에 따라 달라지는 term을 가지고 있지 않다.)

GAN game의 환경과 agent 사이 상호작용은 Fig.4와 같다.

Fig.4. RL setting에서의 GAN game formulated. 이미지들은 binary 이미지이며 action은 픽셀을 1 또는 0으로 설정하는 것과 같다. 환경은 실제 이미지 또는 생성된 이미지를 보여주도록 랜덤하게 선택한다. 환경이 실제 이미지를 선택할 때 agent는 1의 reward를 받고 그게 아니라면 0을 받는다. Agent에 의해 선택된 actions은 reward에 아무런 영향을 주지 않는다.

“GANs은 stateless MDPs에서 blind actor와 수정된 AC method로 볼 수 있다.” – Pfau&Vinyals

 

  GANs과 AC methods 모두 학습 시 불안정하기 때문에, 저자는 몇 안정화를 위한 방법들을 그들의 논문에 적어놨다. 하지만 이 포스팅에서는 게시하지 않을 것이다.